در این پست، ما در مورد انواع مختلف توابع فعال یاد بگیریم؛ ما همچنین می بینیم که کدام تابع فعال تر بهتر از دیگر است. این پست فرض می کند که شما یک ایده اولیه از شبکه های عصبی مصنوعی (ANN) دارید، اما در صورتی که این کار را نکنید، توصیه می کنم ابتدا پست را در مورد درک شبکه های عصبی فیدبک بخوانید.
1. عملکرد فعال سازی چیست؟
شبکه های عصبی زیستی الهام بخش توسعه شبکه های عصبی مصنوعی بودند. با این حال، ANN حتی نمایشی تقریبی از عملکرد مغز نیست. هنوز هم مفید است که ارتباط یک تابع فعال سازی در یک شبکه عصبی بیولوژیک قبل از اینکه ما بدانیم که چرا از آن در شبکه عصبی مصنوعی استفاده می کنیم، قابل درک است.
یک نورون معمولی دارای ساختار فیزیکی است که شامل یک بدن سلولی است، یک آکسون که پیام را به دیگر نورون ها ارسال می کند و dendrites که سیگنال یا اطلاعات از دیگر نورون ها را دریافت می کند.
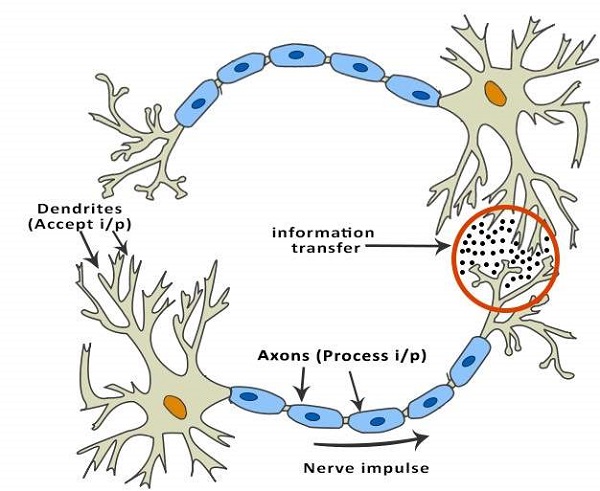
در تصویر بالا، دایره قرمز نشان دهنده منطقه ای است که دو نورون ارتباط برقرار می کند. نورون سیگنال های دیگر نورون ها را از طریق دندریت ها دریافت می کند. وزن (قدرت) مربوط به یک دندریت، به نام وزن سیناپسی، با سیگنال ورودی ضرب می شود. سیگنال های dendrites در بدن سلول انباشته شده و اگر قدرت سیگنال حاصل از آن بالاتر از یک آستانه مشخص باشد، نورون پیام را به آکسون می فرستد. در غیر این صورت، سیگنال توسط نورون کشته می شود و بیشتر منتشر نمی شود.
تابع فعال سازی تصمیم می گیرد که سیگنال را منتقل کند یا نه. در این مورد، یک تابع گام ساده با یک پارامتر واحد – آستانه است. در حال حاضر، هنگامی که ما چیزی جدید (یا چیزی غیرفعال) یاد بگیریم، آستانه و وزن سیناپسی برخی از نورونها تغییر می کنند. این ارتباطات جدیدی را در میان نورون ایجاد می کند که مغز چیزهای جدید را یاد می گیرد.
بگذارید همان مفهوم را دوباره درک کنیم اما این بار با استفاده از نورون مصنوعی.
در شکل بالا، (x_1، \ cdots، x_n) یک بردار سیگنال است که با وزن \ left (w_1، w_2، \ cdots، w_n \ right) ضرب می شود. این به دنبال انباشت (به عنوان مثال جمع شدن + اضافه کردن تعصب b). در نهایت یک تابع فعال f برای این مقدار اعمال می شود.
توجه داشته باشید که وزن \ left (w_1، w_2، \ cdots، w_n \ right) و bias b تبدیل سیگنال ورودی به صورت خطی. از سوی دیگر فعال سازی، سیگنال غیر خطی را تبدیل می کند و این غیر خطی بودن است که به ما امکان می دهد تا تغییرات پیچیده ای را در میان ورودی و خروجی یاد بگیریم.
در طول سالها، توابع مختلف مورد استفاده قرار گرفته اند و هنوز یک منطقه فعال تحقیقاتی برای یافتن یک تابع فعال سازی مناسب است که باعث می شود شبکه عصبی بهتر و سریع تر یاد بگیرد.
2. شبکه چگونه یاد می گیرد؟
ضروری است که یک ایده اساسی در مورد نحوه یادگیری شبکه عصبی بدست آوریم. بیایید بگوییم خروجی مورد نظر از شبکه y است. شبکه خروجی Y تولید می کند. تفاوت بین خروجی پیش بینی شده و خروجی مورد نظر (y – y) به یک متریک شناخته شده به عنوان عملکرد تلفات (J) تبدیل می شود. وقتی شبکه عصبی اشتباهات زیادی را انجام می دهد، از دست دادن بالا است، و زمانی که اشتباهات کمتری انجام می شود کم است. هدف از فرایند آموزش این است که وزن و تعصب را پیدا کنیم که عملکرد تضعیف را در مجموعه آموزشی کاهش می دهد.
در شکل زیر، عملکرد از دست دادن مانند یک کاسه شکل می گیرد. در هر نقطه ای از فرایند آموزش، مشتقات جزئی از کار افتادن w.r.t به وزن، چیزی جز شیب کاسه در آن محل نیست. می توان دید که با حرکت در جهت پیش بینی شده توسط مشتقات جزئی، ما می توانیم به پایین کاسه برسیم و بنابراین عملکرد تلفات را به حداقل برسانیم. این ایده استفاده از مشتقات جزئی یک تابع به منظور تکرار آن حداقل محلی را نام می برد.
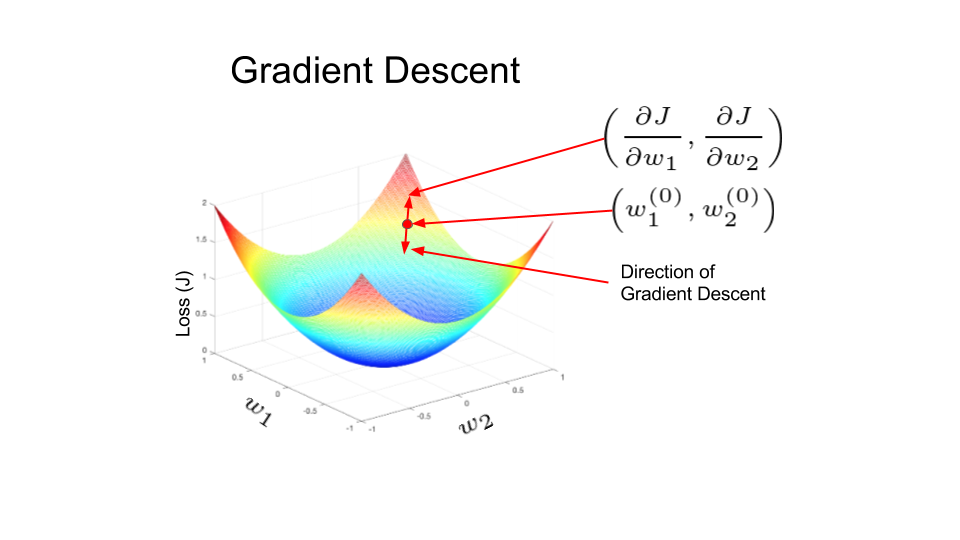
در شبکه های عصبی مصنوعی وزن با استفاده از روش به نام Back propagation به روز می شود. مشتقات جزئی از عملکرد از دست دادن w.r.t وزن برای به روز رسانی وزن استفاده می شود. به یک معنا، خطا در شبکه با استفاده از مشتقات پخش می شود. این کار به صورت تکراری انجام می شود و پس از بسیاری از تکرارها، از دست دادن به حداقل مقدار می رسد و مشتق از دست دادن صفر می شود.
ما قصد داریم جلوی انتشار را در یک پست وبلاگ جداگانه پوشش دهیم. در اینجا اصلی ترین نکته این است که حضور مشتقات در روند آموزش.
3. انواع توابع فعال
تابع فعال سازی خطی: یک تابع خطی ساده از فرم f (x) = x به طور معمول، ورودی به خروجی منتقل می شود بدون هیچ گونه تغییری.
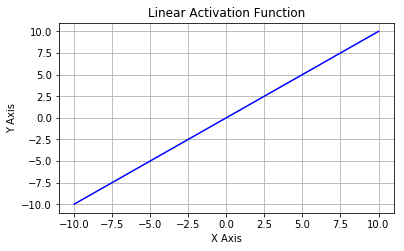
توابع فعال غیرخطی: این توابع برای جدا کردن داده هایی که به صورت خطی قابل جدا شدن نیستند و بیشترین استفاده از توابع فعال سازی هستند استفاده می شود. معادله غیر خطی، نقشه برداری از ورودی ها به خروجی ها را مدیریت می کند. چند نمونه از انواع مختلف توابع فعال سازی غیر خطی عبارتند از sigmoid، tanh، relu، lrelu، prelu، swish، و غیره. ما در مورد تمام این توابع فعال با جزئیات صحبت خواهیم کرد.
4. چرا ما یک تابع فعال سازی غیر خطی در یک شبکه عصبی مصنوعی نیاز داریم؟
شبکه های عصبی برای پیاده سازی توابع پیچیده استفاده می شوند و توابع فعال سازی غیر خطی آنها را قادر می سازد تا توابع مختلط مختلط را تقریب آورند. بدون غیر خطی بودن معرفی شده توسط تابع فعال سازی، چند لایه از یک شبکه عصبی معادل یک شبکه عصبی تک لایه است.
بیایید مثال ساده ای را بدانیم که چرا بدون غیر خطی بودن می توان عملکردهای ساده ای مانند XOR و XNOR را تعریف کرد. در شکل زیر، ما گرافیکی یک دروازه XOR را نشان می دهیم. دو مجموعه در مجموعه داده های ما وجود دارد که نشان دهنده یک صلیب و یک دایره است. وقتی دو ویژگی، X1 و X2 یکسان هستند، برچسب کلاس یک کراس قرمز است، در غیر اینصورت، یک دایره آبی است. دو ردیف قرمز خروجی 0 برای مقدار ورودی (0،0) و (1،1) و دو حلقه آبی دارای خروجی 1 برای مقدار ورودی (0،1) و (1،0) است.
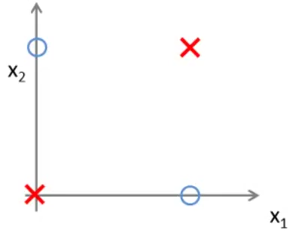
از تصویر بالا می توان دید که نقاط داده به صورت خطی قابل جدا شدن نیستند. به عبارت دیگر، ما نمی توانیم یک خط مستقیم را برای جدا کردن حلقه های آبی و صلیب سرخ از یکدیگر بگیریم. از این رو، ما به یک مرز تصمیم گیری غیر خطی نیاز داریم تا آنها را جدا سازیم.
تابع فعال سازی نیز برای خنثی کردن خروجی شبکه عصبی در محدوده معینی ضروری است. خروجی یک نورون \ sum ^ n_i w_i x_i + b می تواند مقادیر بسیار زیادی داشته باشد. این خروجی، وقتی که به نورون لایه بعدی بدون اصلاح تغذیه می شود، می تواند به اعداد حتی بزرگتر تبدیل شود و بدین ترتیب پردازش را به صورت محاسباتی قابل اجتناب کند. یکی از وظایف تابع فعال سازی این است که خروجی یک نورون را به چیزی که محدود است (به عنوان مثال، بین 0 و 1) محدود کنیم.
با این پس ما آماده هستیم تا انواع مختلفی از توابع فعال سازی را درک کنیم.
5. انواع توابع فعال سازی غیر خطی
5.1 سیگموئید
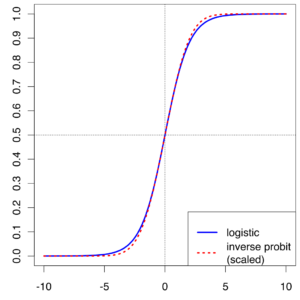
همچنین به عنوان تابع فعال سازی لجستیک شناخته می شود. یک عدد ارزش واقعی طول می کشد و آن را در محدوده بین 0 و 1 قرار می دهد. همچنین در لایه خروجی استفاده می شود که هدف آن هدف پیش بینی احتمال است. این اعداد منفی بزرگ را به 0 و عدد مثبت بزرگ به 1 تبدیل می کند. به صورت ریاضی به عنوان نشان داده شده است
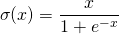
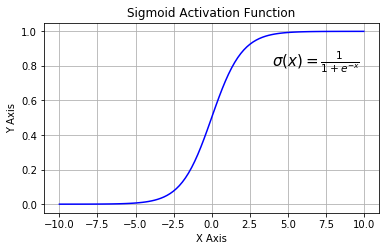
شکل زیر نمودار عملکرد سیگموئید و مشتق آن را به صورت گرافیکی نشان می دهد

سه ضعف اصلی سیگموئید عبارتند از:
شیب ناپایدار: توجه کنید که تابع سیگموئید نزدیک به 0 و 1 مسطح است. به عبارت دیگر، گرادیان سیگموید 0 در نزدیکی 0 و 1 است. در طول بازگشت از طریق شبکه با فعال شدن سیگموئید، گرادیان در نورون هایی که خروجی آنها نزدیک 0 یا 1 تقریبا 0. این نورون ها نورون های اشباع نامیده می شوند. بنابراین، وزن این نورون ها به روز نمی شود. نه تنها این، وزن نورون هایی که به این نورون ها متصل هستند نیز به آرامی به روز می شوند. این مشکل همچنین به عنوان گرادیان ناپایدار شناخته شده است. بنابراین، تصور کنید اگر یک شبکه بزرگ شامل نورون های سیگموئید وجود داشته باشد که بسیاری از آنها در یک رژیم اشباع قرار دارند، شبکه نمی تواند به عقب رانده شود.
صفر مرکز: خروجی های Sigmoid صفر محور نیستند.
محاسبه گران: عملکرد exp () در مقایسه با سایر توابع فعال سازی غیرخطی گران محاسباتی گران است.
تابع فعال سازی غیر خطی بعدی که من میخواهم بحث کنم به مشکل صفر محور در سیگموئید می پردازد.
5.2. Tanh

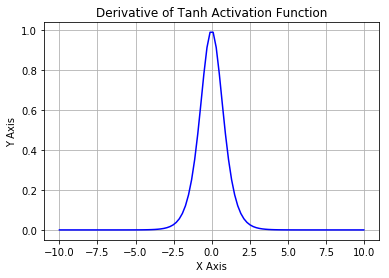
همچنین به عنوان تابع فعال سازی مماسی هذلولی شناخته می شود. همانند sigmoid، tanh نیز یک عدد ارزش واقعی را می گیرد، اما آن را به محدوده بین -1 و 1 تقسیم می کند. بر خلاف سیگموئید، خروجی های tanh صفر محور هستند، زیرا محدوده بین -1 و 1 است. شما می توانید از یک تابع tan به عنوان دو سیگموئید با هم قرار گرفته اند. در عمل، tanh بیش از sigmoid ترجیح داده است. ورودی های منفی که به عنوان منفی بسیار منفی، ارزش ورودی صفر به صفر نزدیک می شوند و ورودی های مثبت در نظر گرفته شده اند. تنها نکته تانش این است:
تانن تابع نیز از مشکل شیب گسیختگی رنج می برد و در نتیجه اشباع می شود.
برای رسیدگی به مسئله گرادیان ناپدید شده، اجازه دهید ما در مورد یکی دیگر از تابع فعال سازی غیر خطی شناخته شده به عنوان واحد خطی تصحیح (ReLU) که بسیار بهتر از دو توابع فعال قبلی است و بیشتر در این روز استفاده می شود.
5.3. Rectified Linear Unit (ReLU)

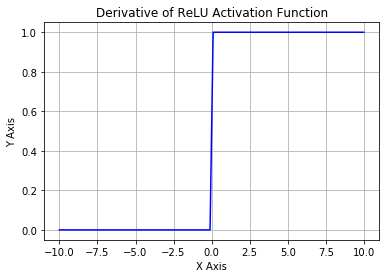
همانطور که می توانید از شکل بالا بدانید، ReLU از پایین به نصف رفع شده است. از نظر ریاضی، از این عبارت ساده استفاده می شود
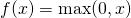
این به این معنی است که هنگام ورودی x <0 خروجی 0 است و اگر x> 0 خروجی x باشد. این فعال شدن باعث می شود که شبکه خیلی سریعتر هماهنگ شود. این اشباع نمی کند، به این معنی است که آن را در برابر مسئله شیب گسیختگی حداقل در ناحیه مثبت (زمانی که x> 0) مقاوم است، بنابراین نورون ها تمام صفر را در حداقل نیمی از مناطق خود تکثیر نمی کنند. ReLU محاسباتی بسیار کارآمد است زیرا با استفاده از آستانه ساده ساده سازی شده است. اما نقاط ضعف Neuron ReLU وجود دارد:
صفر محور: خروجی ها صفر محور مانند تابع فعال سازی sigmoid نیستند.
مسئله دیگر با ReLU این است که اگر x <0 در طول پاس رو به جلو، نورون غیر فعال باقی بماند و در طول گذر عقب، گرادیان را از بین می برد. بنابراین وزن ها به روز نمی شوند و شبکه یاد نمی گیرد. هنگامی که x = 0، شیب در آن نقطه تعریف نشده است، اما این مشکل در حین اجرای با انتخاب چارچوب یا شیب سمت راست مورد توجه قرار گرفته است.
برای رفع مسئله گرادیان ناپدید در تابع فعال سازی ReLU زمانی که x <0 ما چیزی به نام Leaky ReLU داشتیم که تلاش برای رفع مشکل ReLU مرده بود. بیایید دقیق ReLU نشت را درک کنیم.
5.4. Leaky ReLU

این تلاش برای کاهش مشکل ReLU در حال مرگ بود. تابع محاسبه می کند

مفهوم ReLU نشت زمانی است که x <0، آن یک شیب مثبت کوچک 0.1 را دارد. این کار تا حدی مشکل ReLU در حال مرگ را از بین می برد، اما نتایج به دست آمده با آن سازگار نیستند. اگرچه تمام خصوصیات یک تابع فعال سازی ReLU، به عنوان مثال، کارآیی محاسباتی، بسیار سریع تر هماهنگ می شود، در منطقه مثبت اشباع نمی شود.
ایده ReLU نشتی را می توان حتی بیشتر گسترش داد. به جای ضرب x با یک اصطلاح دائمی، می توان آن را با یک پارامتر ضرب کردیم که به نظر می رسد ReLU نشتی بهتر کار می کند. این فرمت به ReLU نشت داده شده به عنوان پارامتریک ReLU شناخته می شود.
5.5 پارامتریک ReLU

عملکرد PReLU توسط داده می شود
کجا \ alpha یک hyperparameter است. ایده در اینجا این بود که یک hyperparameter \ alpha خودسرانه را معرفی کنیم و این \ alpha را می توان یاد گرفت زیرا شما می توانید به آن بازگردید. این باعث می شود که نورون ها توانایی انتخاب شیله ای را در منطقه منفی داشته باشند و با این توانایی، آنها می توانند ReLU یا ReLU نشت کنند.
به طور خلاصه، بهتر است از ReLU استفاده کنید، اما می توانید با Leaky ReLU یا پارامتریک ReLU آزمایش کنید تا ببینید آیا نتایج بهتر شما برای مشکل شما فراهم می شود
5.6. SWISH
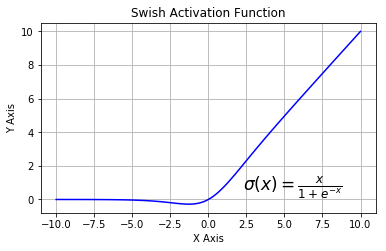
به تازگی توسط محققان در Google منتشر شده است که همچنین به عنوان یک تابع فعال سازی خود به خود شناخته شده است. از نظر ریاضی، آن را به عنوان نشان داده شده است
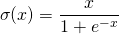
بر طبق این مقاله، تابع فعال SWISH بهتر از ReLU انجام می شود
از شکل بالا می توان دید که در ناحیه منفی محور x شکل دم از تابع فعال سازی ReLU متفاوت است و به همین دلیل خروجی از عملکرد Activation Swish حتی ممکن است حتی زمانی که مقدار ورودی افزایش می یابد کاهش یابد. اکثر توابع فعال یکسان هستند، به عنوان مثال، مقدار آنها هرگز به دلیل افزایش ورودی کاهش نمی یابد. Swish دارای ویژگی محدودیتی یک طرفه در صفر است، صاف و یکنواخت نیست. جالب خواهد بود بدانید که با تغییر تنها یک کد از کدام کار، آن را انجام می دهد.